Electricidad its - Ley de Ohm

Ley de Ohm

Circuito mostrando la Ley de Ohm: Una fuente eléctrica con una diferencia de potencial V, produce una corriente eléctrica I cuando pasa a través de la resistencia R

La ley de Ohm, es una propiedad específica de ciertos materiales. La relación

$V=Icdot R,$

es un enunciado de la ley de Ohm. Un conductor cumple con la ley de Ohm sólo si su curva V-I es lineal; esto es si R es independiente de V y de I. La relación

$R=frac{V}{I}$

sigue siendo la definición general de la resistencia de un conductor, independientemente de si éste cumple o no con la ley de Ohm. La intensidad de la corriente eléctrica que circula por un dispositivo es directamente proporcional a la diferencia de potencial aplicada e inversamente proporcional a la resistencia del mismo, según expresa la fórmula siguiente:

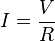
$I=frac{V}{R}$

En donde, empleando unidades del Sistema internacional:
I = Intensidad en amperios (A)
V = Diferencia de potencial en voltios (V)
R = Resistencia en ohmios (Ω).

Enunciado

En un conductor recorrido por una corriente eléctrica, el cociente entre la diferencia de potencial aplicada a los extremos del conductor y la intensidad de la corriente que por él circula, es una cantidad constante, que depende del conductor, denominada resistencia.

La ley enunciada verifica la relación entre voltaje y corriente en un resistor.

Historia

El científico Georg Simon Ohm, mientras experimentaba con materiales conductores, como resultado de su investigación, llegó a determinar que la relación entre voltaje y corriente era constante y nombró a esta constante resistencia.

Esta ley fue formulada por Georg Simon Ohm en 1827, en la obra Die galvanische Kette, mathematisch bearbeitet (Trabajos matemáticos sobre los circuitos eléctricos), basándose en evidencias empíricas. La formulación original, es:

$vec J={sigma}{vec E}$

Siendo $vec J$ la densidad de la corriente, $σ$ la conductividad eléctrica y $vec E$ el campo eléctrico, sin embargo se suele emplear las fórmulas simplificadas anteriores para el análisis de los circuitos

Deducción

Como ya se destacó anteriormente, las evidencias empíricas mostraban que ${vec J}$ (vector densidad de corriente) es directamente proporcional a $vec E$ (vector campo eléctrico). Para escribir ésta relación en forma de ecuación, es necesario añadir una constante arbitraria, que posteriormente se llamó factor de conductividad eléctrica, que representaremos como σ. Entonces:

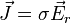
$vec J={sigma}{vec E_{r}}$

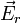El vector $vec E_{r}$ es el vector resultante de los campos que actúan en la sección de alambre que se va a analizar; es decir, del campo producido por la carga del alambre en sí y del campo externo, producido por una batería, una pila u otra fuente de fem. Por lo tanto:

$frac{vec J}sigma={vec E + vec E_{ext}}$

Ahora, sabemos que $vec J = frac{I}{A}vec n$ , donde $vec n$ es un vector unitario de dirección, con lo cual reemplazamos y multiplicamos toda la ecuación por un $dvec l$ :

$frac{I}{Asigma}vec n cdot dvec l = ({vec E cdot dvec l + vec E_{ext} cdot dvec l})$

Los vectores $vec n$ y $dvec l$ poseen la misma dirección y sentido, con lo cual su producto escalar puede expresarse como el producto de sus magnitudes por el coseno del ángulo formado entre ellos. Es decir:

Por lo tanto, se hace la sustitución:

$frac{I}{Asigma} dl = ({vec E cdot dvec l + vec E_{ext} cdot dvec l})$

Integrando ambos miembros en la longitud del conductor:

$int_{1}^{2} frac{I}{Asigma} dl = int_{1}^{2}({vec E cdot dvec l + vec E_{ext} cdot dvec l}) = int_{1}^{2}{vec E cdot dvec l} + int_{1}^{2}{vec E_{ext} cdot dvec l}$

El miembro derecho representa el trabajo total de los campos que actúan en la sección de alambre que se está analizando, y de cada integral resulta:

$int_{1}^{2}{vec E cdot dvec l} = phi_{1} - phi_{2}$

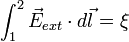
$int_{1}^{2}{vec E_{ext} cdot dvec l} = xi$

Donde $φ 1 - φ 2$ representa la diferencia de potencial entre los puntos 1 y 2, y $ξ$ representa la fem; por tanto, podemos escribir:

$frac{I}{Asigma} l_{12} = phi_{1} - phi_{2} + xi = U_{12}$

donde $U 12$ representa la caída de potencial entre los puntos 1 y 2.

Como dijimos anteriormente, σ representa la conductividad, por lo que su inversa representará la resistividad, y la representaremos como ρ. Así:

$frac{Irho}{A} l_{12} = U_{12}$

Finalmente, la expresión 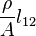$frac{rho}{A} l_{12}$ es lo que se conoce como resistencia eléctrica

Podemos escribir la expresión final:

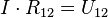
$Icdot R_{12} = U_{12}$

Este sitio web fue creado de forma gratuita con PaginaWebGratis.es. ¿Quieres también tu sitio web propio?

Registrarse gratis